G2实现大数据展示模块

Last updated on May 6, 2024 am

摘要

本次回顾了业务需求里大数据模块的实现过程。该项目发布以后之前有投屏在公司大屏上，某天偶然经过以后看了很自豪啊哈哈。回顾心路历程，从接到需求后恶补正态分布函数，到技术选型中途从D3转向G2，再到G2图表实现到80%以后，发现其动效方面API能力不足之后硬核做完以后可谓一波三折，该需求一共做了6天，今天刚好回顾一下，正好也可以和之前开发使用过的eChart、D3做一个简单的对比。

一、需求分析

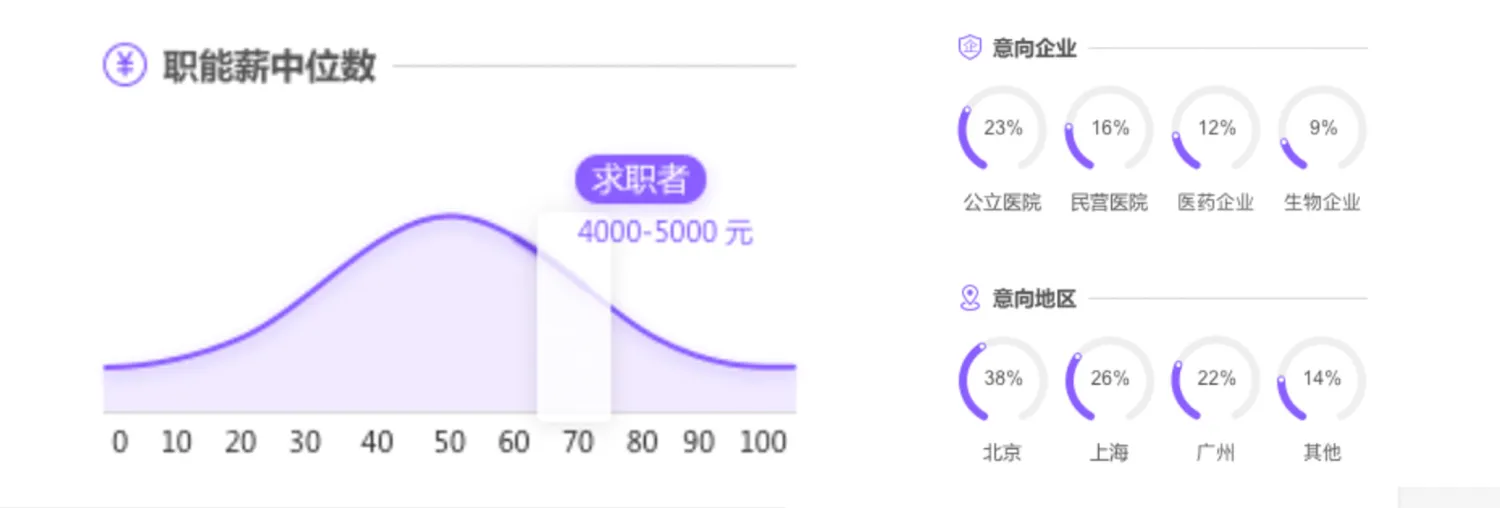
需求很简单，大数据模块需要前端画两个图，一个是面积曲线图、一个是环形进度条。

面积曲线图

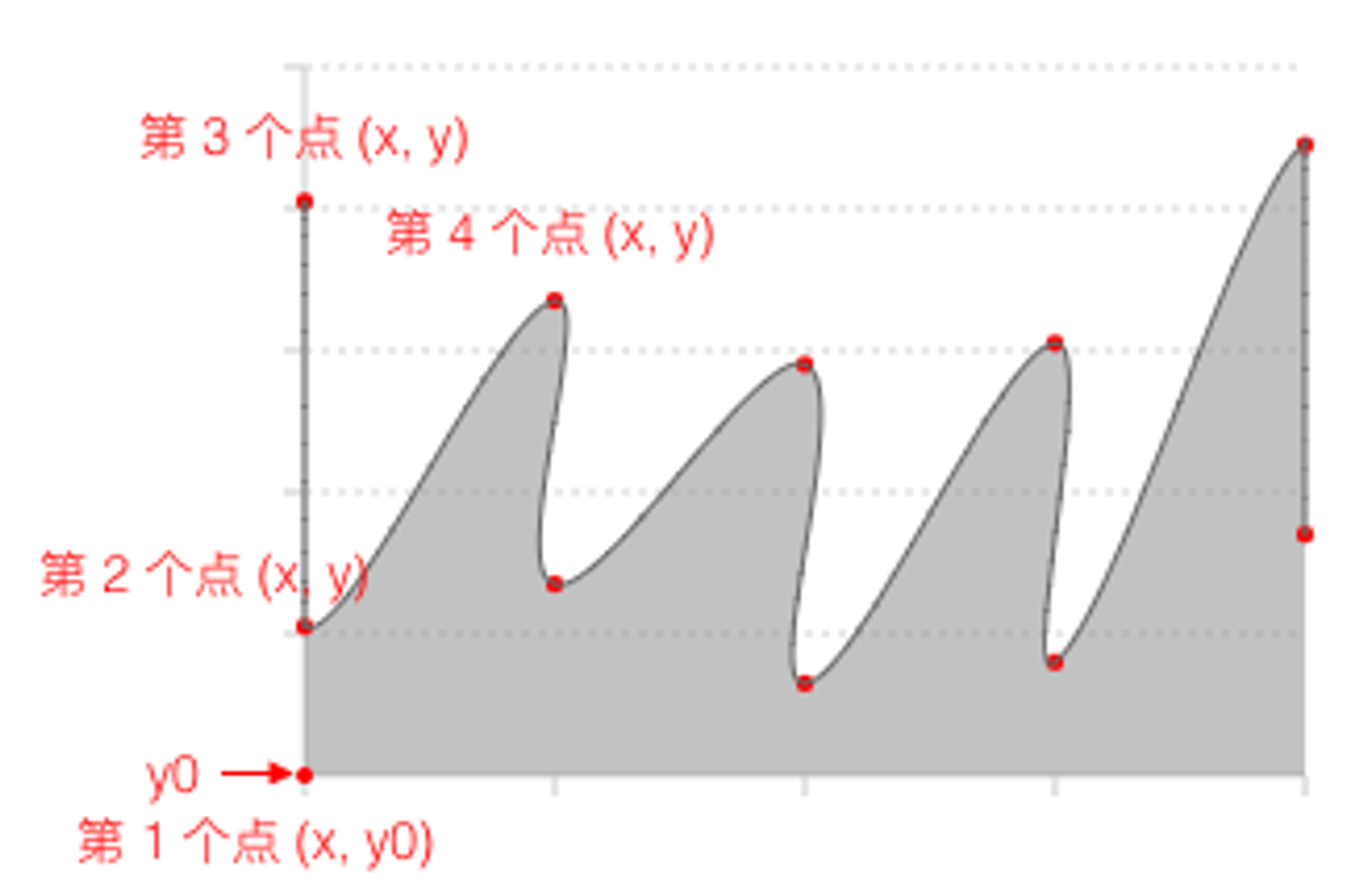
面积曲线图需要使用曲线绘制出固定的走势
线条和面积的阴影颜色不同
初次渲染时需要有自左向右的进入动画
相应数值处标注起求职者的薪水位置

环形进度条

数据大小使用环形进度条百分比呈现
初次进入时有个数据增长的动效。
环形进度条有个白色圆跟着动

emmmm….需求看起来好像不过分

示例

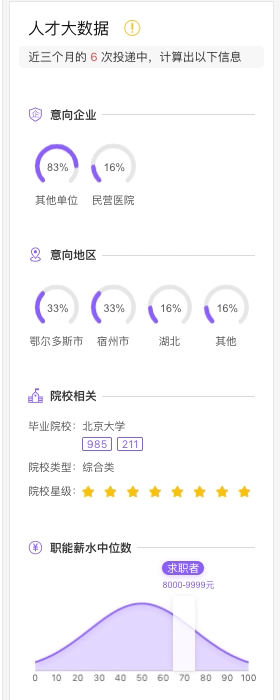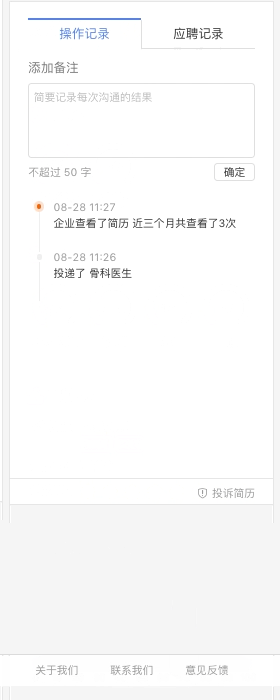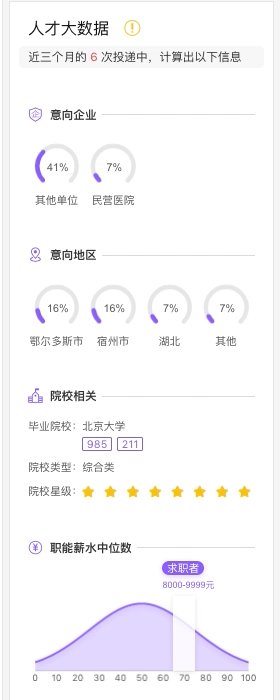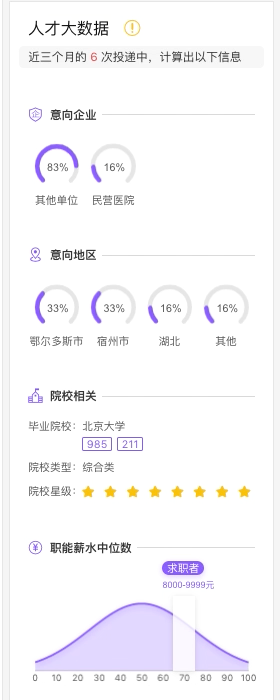
二、画图届的PK

听到数据可视化需求，马上脑袋里出现三大框架，~~vue，react、angular~~，是 echart、G2、D3。

多而全的EChart

以前用echart做过移动端的饼图和折线图，而echart作为一款开箱即用的图表库，确实很方便，但是echart的定制能力比较弱，对于这么简单的图估计光查api和删减配置项就要弄很久，而且最后是否能还原到设计稿这样样式应该是个问号？不过之所以用惯了echart的一步到位，也想探究下画图更加偏底层的内容。

陡峭的D3

G2是画图届的面团，可定制化能力比echart相对高，用它来实现应该没问题。好，那我还是用D3吧，这样我就可以给大家写一篇D3的分享了，不过大家也发现了，最终文章的标题是讲 G2而不是D3，因为在D3上碰壁了。

我们简单说一下D3和G2的区别，D3简称“画图届的jquery”，因为D3是基于SVG的，而G2则是基于Canvas（当然3.2.7版本也开始支持以SVG渲染），两者其实各有优缺点，「数据可视化小组」最近搬运的这篇文章

《选择Canvas还是SVG》简单介绍了Canvas 和 SVG的适用场景和性能差异。

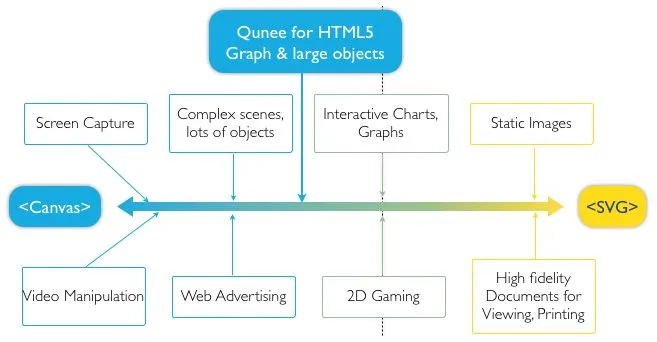
简单摘录一下：

如果单就图表库的视角来看，选择 Canvas 和 SVG 各有千秋。小画布、大数据量的场景适合用 Canvas，譬如热力图、大数据量的散点图等。如果画布非常大，有缩放、平移等高频的交互，或者移动端对内存占用量非常敏感等场景，可以使用 SVG 的方案。

为什么初期使用D3不是一个好的选择？

好了，接下来我们说一说为什么刚上来就使用D3不是一个好的选择？

首先你得储备大量SVG相关的知识，但如果你之前没接触过SVG绘图的话，就会花大量的时间成本下去，

D3主要是和DOM交互，比如SVG有六大预设图形：矩形rect、圆形circle、椭圆ellipse、线条line、折线polyline、多边形polygon，另外再加一个万能的路径path

当你决定使用D3画图时，你就会不能避免的接触这些标签的绘图属性，特别是当你要使用这么一堆属性来绘图的时候，你还得去学每个图形的属性，那真的是会增加很多时间成本。当然，D3已经帮你做了很多封装，即使这样我还是觉得要了解太多SVG的知识，才能把一个图画好。比如我们看一个简单的示例

这个其实就有点类似于用CSS3动画去实现复杂的H5动画，这一点其实我还是建议使用可视化的方式去调整，之前项目里我做过一个带路径的体验地图（红框部分），其路径就是直接通过设计稿sketch生成的，路劲的行径动效则是根据数值的百分比的位置计算出来的，光这个动效从预研到实现用了2天。

其次，还需要掌握一些算法和数学函数，比如这次画这个像抛物线（后面会讲），画圆弧，这些SVG固然有很多预设可以选，但是你要让他们动起来，就必须使用 path，而path几乎是一个点一个点绘制的，这才造就了SVG的无限可能。

这是我中途放弃D3的原因。

当然，使用D3比纯用JS去操作SVG还是有其优势的，这个后面再单独开一章节讲。

三、用G2把图画好

面积图

你使用G2的话，其实有一种找回echart的感觉, 通过官网去找示例，面积图比较符合我们的诉求，通过简单的chart.line() 就能绘制出平滑的曲线。

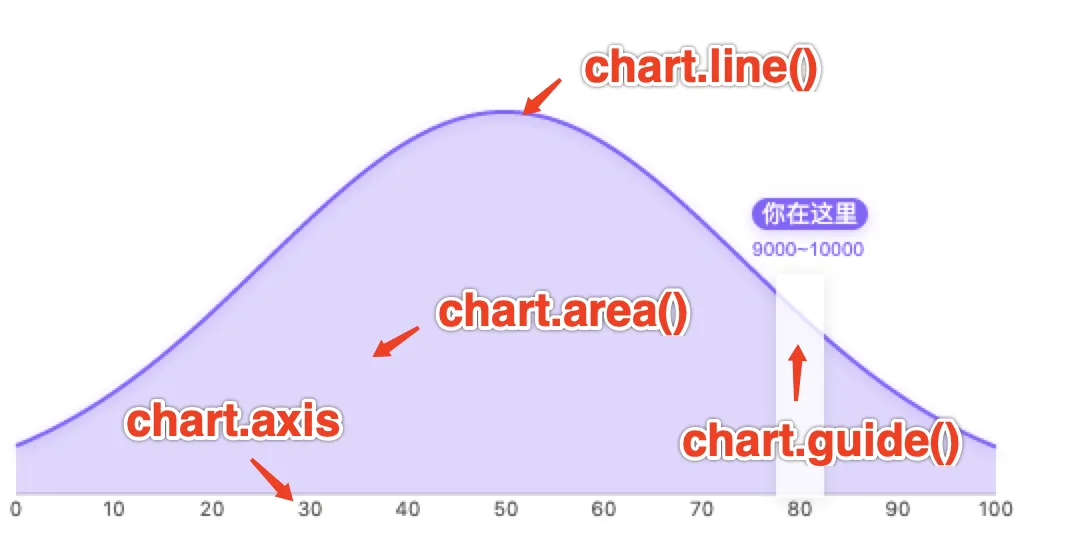
这个图的难点在于以下三个方面：

曲线部分，因为要画出类似设计稿的平滑曲线，所以就不能只使用几个点的标记，我们需要一连串的坐标，这次得益于算法组的帮助，告诉我这是一条正态分布曲线图。
数据部分，因为事先定义好了使用正态分布曲线，那么具体标注的地方就是相应的坐标，后端传入数据的区间为 -2.5 ~ 2.5，需要将坐标映射到 0 ~100 的图中。

正态分布函数

我们先来回顾看下一般正态分布函数的定义，搜了全网，恶补了高数的知识，它的定义是这样的：

若随机变量X服从一个数学期望为μ、方差（σ^2）的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

它的函数大概长这样

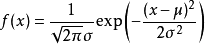
画到图形上

一般正态分布函数

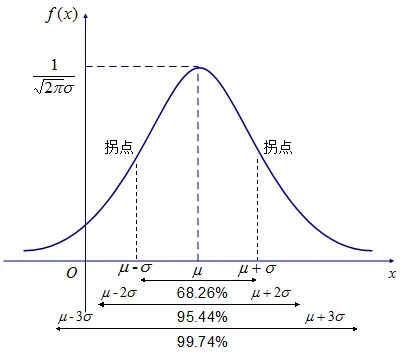
μ = 0,σ = 1，为标准正态分布

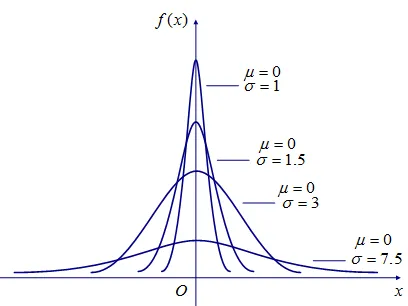
这里我们要关注几个参数：

1μ（平均值）决定了最高点的位置x轴上的偏移量。
2σ（标准差）决定了这个函数的陡峭还是平缓, σ越小，函数越陡峭
μ - n*σ 可以划定函数的边界

正态分布函数使用JS表达：

 // x: x的值
 // mean: 平均数
 // std: 标准差
function lineGenerate(x, mean, std) {
    return (
      (1 / (std * Math.sqrt(Math.PI * 2))) * Math.exp(-(Math.pow(x - mean, 2) / (2 * Math.pow(std, 2))))
    )
}

数据映射

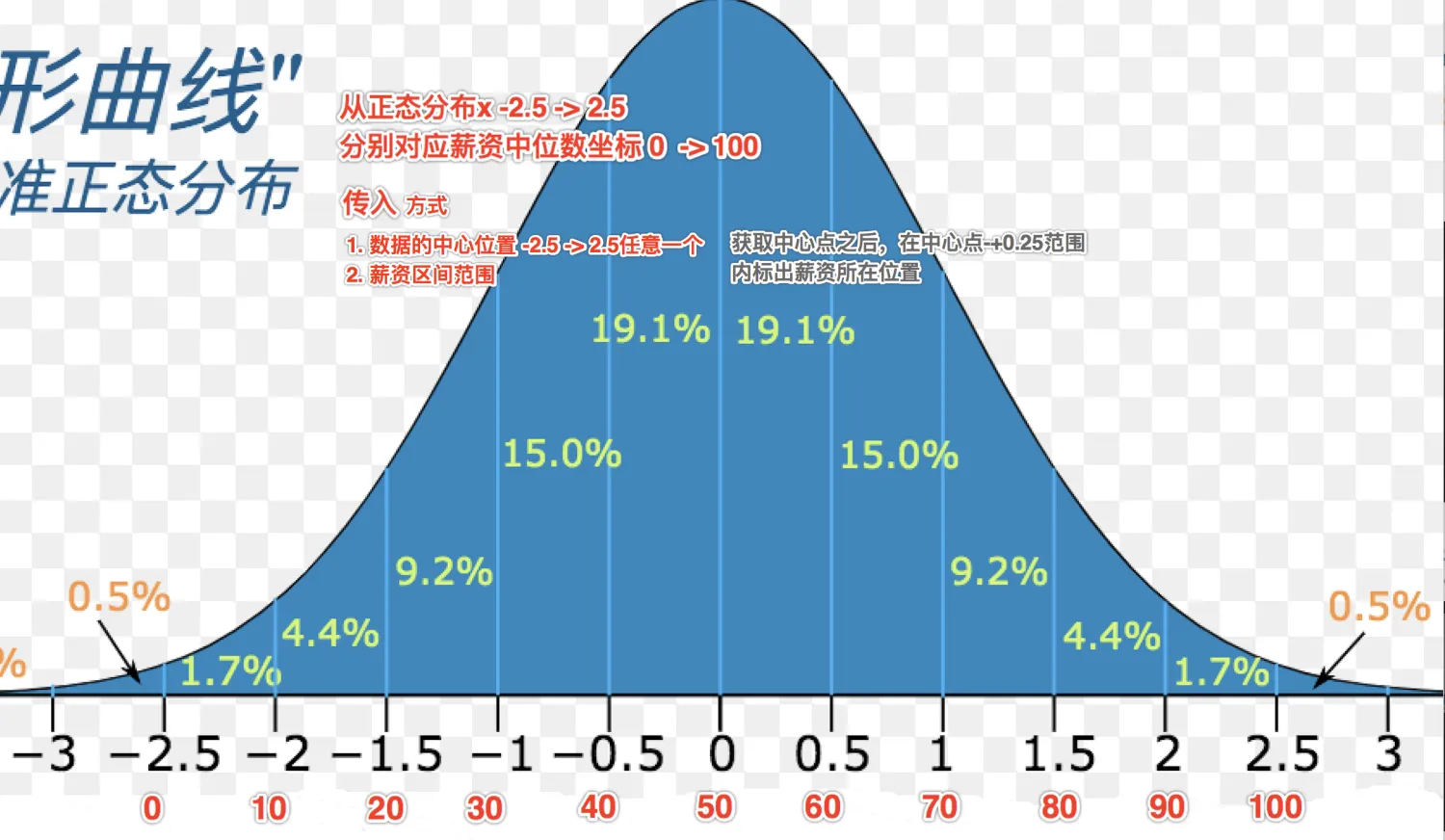
通过将 -2.5 ~ 2.5 的接口数据，映射到 0~100 我们通过方程计算得知

// x 为输入值 
function scaleMap(x) {
    return Math.round((20 * x) + 50)
  }

图例动态高度

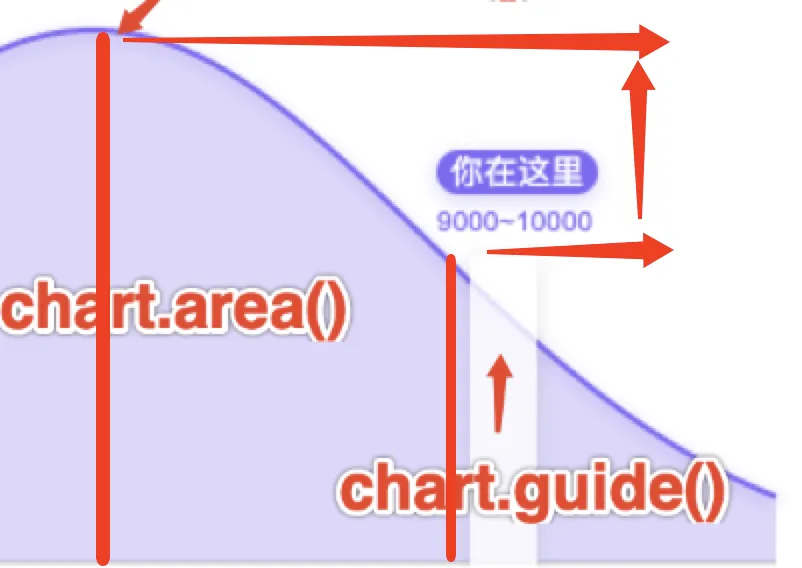
图例部分是使用dom实现的，这部分由G2的 chart.guide() API 提供，它的宽高都是像素px，这边我们没定义相应的数据到尺寸的比例尺，因为基本没用上，所以这部分稍微偷了下懒，毕竟在pc端也没有响应式缩放，所以就给对应的坐标乘以了一个系数去实现类似的根据不同的数据展示不同的高度。

html片段：

1	`*<div class="region" style="width:23.8px;height:${lineGenerate(drawX) adjustValue}px;">**`

javascript片段：

**//计算和中心点的偏移量 ，距离中心点约远，系数越小
    if (Math.abs(drawX - 50) < 10) {
      adjustValue = 16200
    } else if (Math.abs(drawX - 50) < 20) {
      adjustValue = 16000
    } else if (Math.abs(drawX - 50) < 30) {
      adjustValue = 15000
    } else {
      adjustValue = 14500
    }**

完整示例：codePen - areaChart

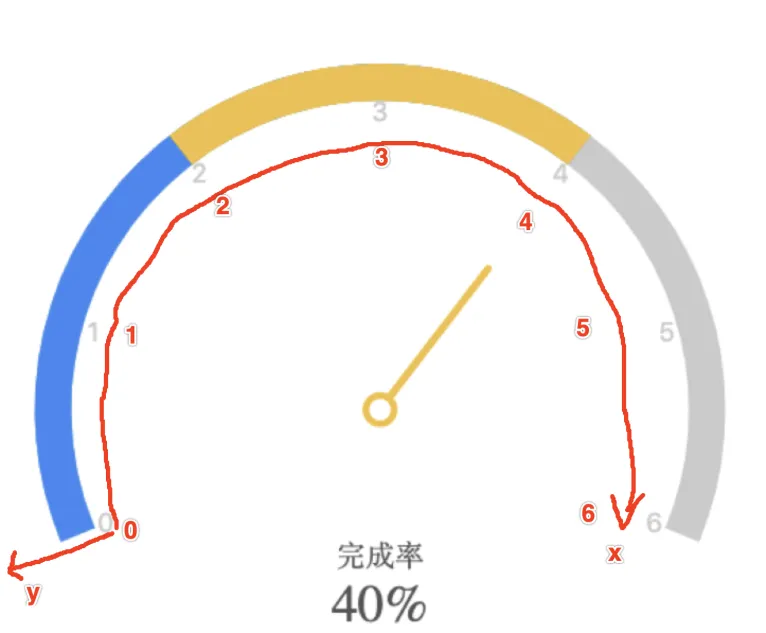
环形进度条

而绘制环形进度条我参考了G2-仪表盘结果半天没写出来，主要是这个仪表盘使用了取巧的办法，其实质上还是使用了chart去做，对坐标轴采用了极坐标的变换，所以看上去像环形进度条，最难实现的就是首末两段的圆角部分，切差距比较大，遂弃。

注册自定义图形

但是G2除了能绘制图表以为，还通过了Shape.shape实现了自定义图形的绘制，具体有以下几种

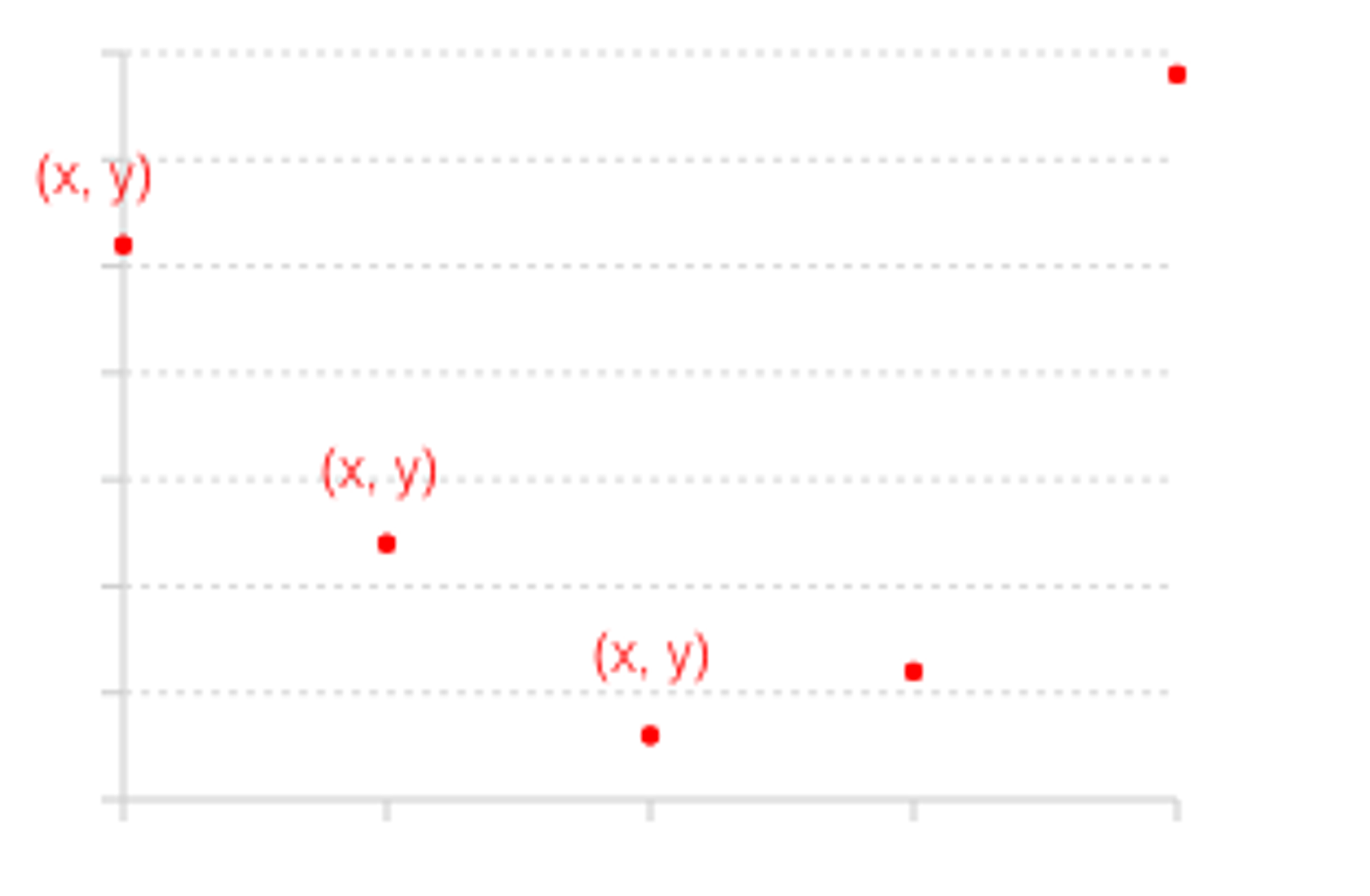
point：点的绘制很简单，只要获取它的坐标以及大小即可，其中的 size 属性代表的是点的半径。

line：线其实是由无数个点组成，在 G2 中我们将参与绘制的各个数据转换成坐标上的点然后通过线将逐个点连接而成形成线图，其中的 size 属性代表的是线的粗细。

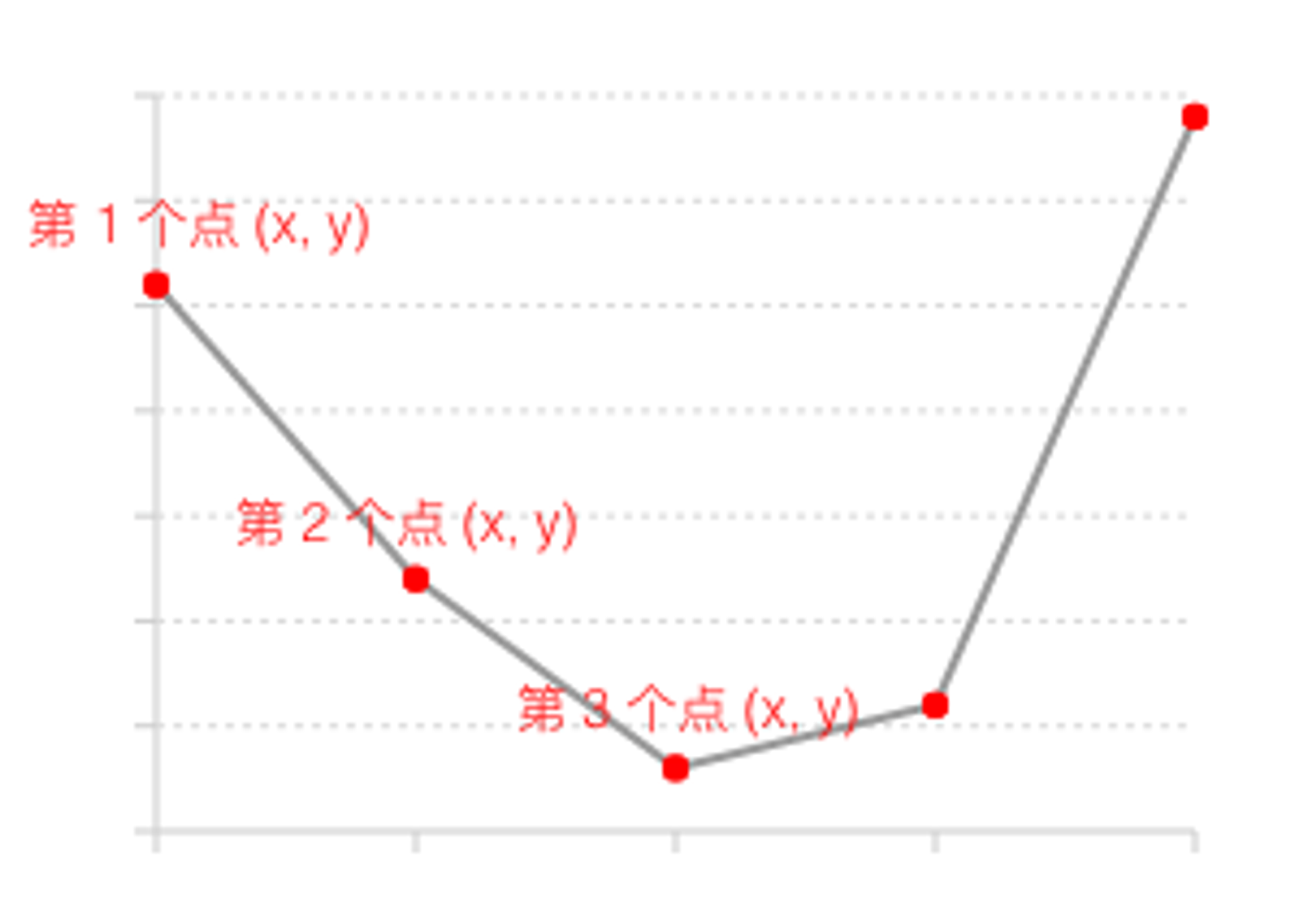
area：area 面其实是在 line 线的基础之上形成的, 它将折线图中折线与自变量坐标轴之间的区域使用颜色或者纹理填充。

interval：interval 默认的图形形状是矩形，而矩形实际是由四个点组成的，在 G2 中我们根据 pointInfo 中的 x、y、size 以及 y0 这四个值来计算出这四个点，然后顺时针连接而成。

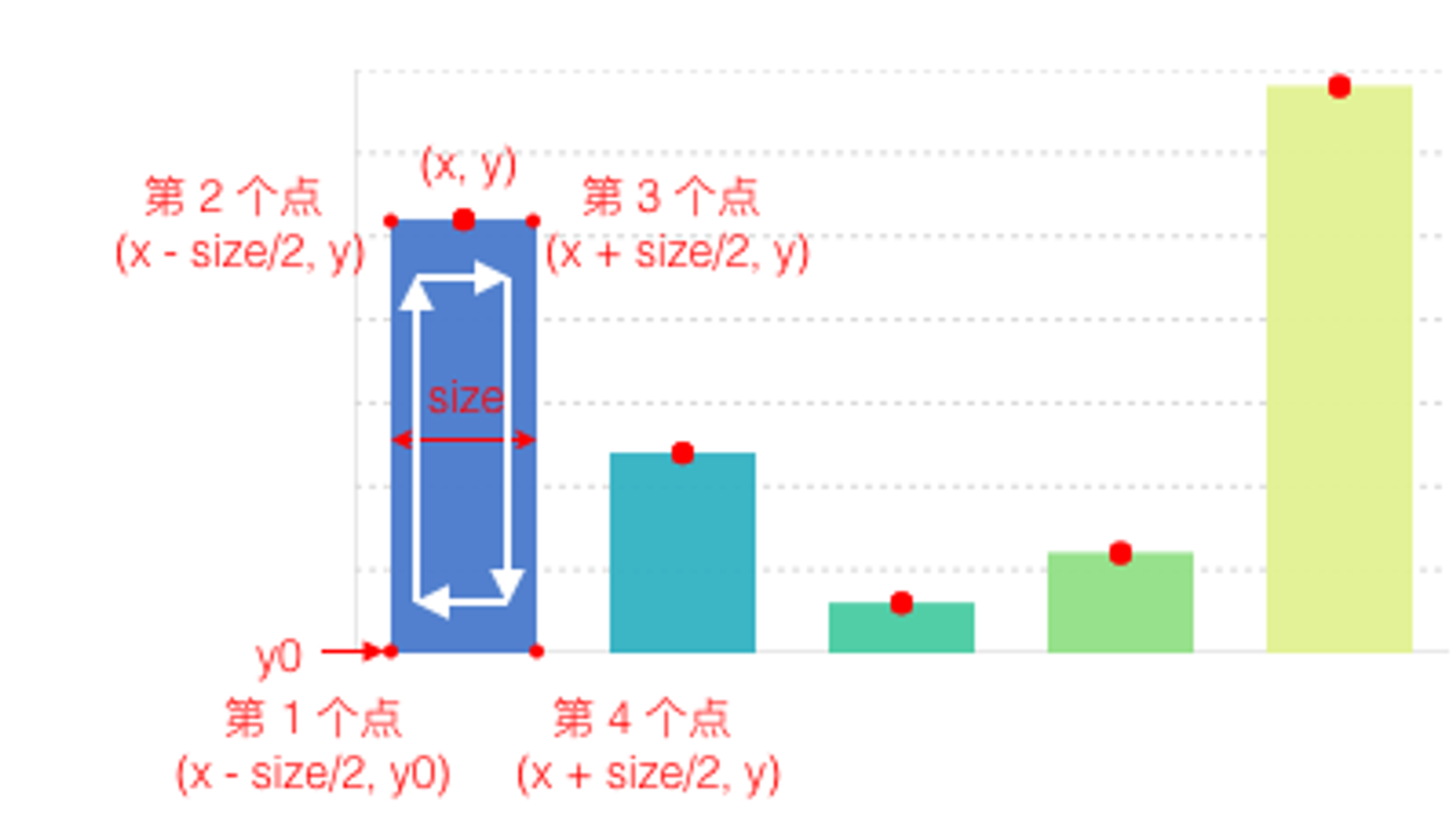
polygon：polygon 多边形其实也是由多个点连接而成，在 pointInfo 中 x 和 y 都是数组结构。

schema：schema 作为一种自定义的几何图形，在 G2 中默认提供了 box 和 candle 两种 shape，分别用于绘制箱型图和股票图，注意这两种形状的矩形部分四个点的连接顺序都是顺时针，并且起始点均为左下角，这样就可以无缝转换至极坐标。

edge：edge 边同 line 线一致，区别就是 edge 是一个线段，连接边的两个端点即可。

于是查了找遍全网，找了半天文档，终于发现了原来 G2.Shape.registerShape 是可以实现的，但是文档和相关demo少的可怜，接下来的画图真的是硬核写完的。

定义带有圆角的5px的线的预设

const Shape = G2.Shape // 环形图自定义形状
const Animate = G2.Animate

   Shape.registerShape('edge', 'arc2', {
     draw: function draw(cfg, group) {

	// 将0-1空间的坐标转换为画布坐标，this.parsePoint 真的太宝贵了，一般人找不到他
       const center = this.parsePoint({ x: 0, y: 0 })

	// 算出圆的最大半径
       const R = this.parsePoint({ x: 0, y: 1 }).y - center.y
       const lineWidth = 5

       //这边定义预设
       return group.addShape('arc', {
         attrs: {
           x: center.x,
           y: center.y,
           r: (R + lineWidth),
           startAngle: (3 / 4) * Math.PI,
           endAngle: (1 / 4) * Math.PI,
           stroke: '#8B5EFF',
           lineWidth,
           lineCap: 'round'
         }
       })
     }
   })

新起一个chart，使用极坐标变换

const chart = new G2.Chart({
  container: wrapEl,
  forceFit: true,
  height: 60,
  padding: [0, 0, 0, 0]
})

chart.source(data)

chart.coord('polar', {
  startAngle: (3 / 4) * Math.PI,
  endAngle: (1 / 4) * Math.PI,
  radius: 0.85
})

绘制灰色圆弧背景

chart.guide().arc({
  zIndex: 0,
  top: false,
  start: [0, 0.945],
  end: [100, 0.945],
  style: {
    // 底灰色
    stroke: '#E5E5E5',
    lineWidth: Piechart.lineWidth,
    lineCap: 'round'
  }
})

绘制显示的进度条并指定动画名称

这边有点坑，我们发现动画执行过程中只有动画完成时的callback，而antV同款可视化组件，F2则提供了update()的回调，这意味着增长的动画效果需要我们自己做。

chart
    .edge()
    .shape('arc2')
    .position('value*1')
    .animate({
      appear: {
        animation: 'stepPercent', // 动画名称
        easing: 'easeQuadInOut', // 动画缓动效果
        delay: 100, // 动画延迟执行时间
        duration: 1000, // 动画执行时间
        callback() {
          // console.log('动画结束')
        }
      }
    })
    .active(false)
    .select(false)

注册一个增长动画效果的开始状态和结束状态

// 注册百分比动画
Animate.registerAnimation('appear', 'stepPercent', (shape, animateCfg) => {
  const startAngle = shape.attr('startAngle')

  // 设置初始状态
  shape.attr('endAngle', (-2 * Math.PI) + startAngle)

  const endX = shape.get('origin').points[0].x
  shape.animate(
    {
      endAngle: ((3 / 2) * Math.PI * endX) - ((5 / 4) * Math.PI)
    },
    animateCfg.duration,
    animateCfg.easing,
    animateCfg.callback,
    animateCfg.delay
  )

  //   console.log('开始做动画')
  $number = $(`#number-${wrapEl}`)
  gainPercent()

})

requestAnimationFrame注册的步进动画

因为电脑缘故，性能低下的CPU可能在1秒内执行不完60帧，所以使用requestAnimationFrame，另外因为 data[0].value / 60 是个不精准的数值，所以会出现最后累加出现不等于传入值的情况，在最后一个次累加等于正常值

let $number
let i = 0
const gainPercent = function() {
  i++
  // 执行到最后一步强制拉到传入的最终值
  if (i === 60) {
    $number.text(`${data[0].value}%`)
  } else {
    const step = data[0].value / 60
    const value = $number.attr('data-val')
    $number.attr('data-val', +value + step)
    $number.text(`${(+value + step).toString().split('.')[0]}%`)
  }

  // console.log(`动画执行${i}`, $number.attr('data-val'))

  if (i < 60) {
    requestAnimationFrame(gainPercent)
  }
}

完整示例：G2-Circle

四、后记

选择可视化框架时按实现的简单程度：echart > G2 > D3 > 原生
echart大而全，但是定制能力比较弱
G2适合实现一些本身就有的图表库，单独去定义自定义图形API和文档较少
G2的动画和联动能力较弱，推荐F2

Tech

#G2 #Canvas #SVG

G2实现大数据展示模块

http://example.com/2019/09/05/G2实现大数据展示模块/

Author

Daniel Chan

Posted on

September 6, 2019

Licensed under

基于多页项目的微前端改造 Previous